

| Hyper limits | |
|---|---|
|
|
|
|
munroburton
Posts: 2379
|
How are they calculated?
http://infodump.thefifthimperium.com/en ... ngton/93/1 With black holes in the news recently, I'm curious about the hypothetical scaling of hyper limits for objects measured in millions and billions of solar masses. |
| Top | |
| Re: Hyper limits | |
|---|---|
|
|
|
|
Jonathan_S
Posts: 9156
|
Plotting the numbers from that table against the solar masses of the stars involved[1] there seems to be a pretty significant inflection point around 1 solar mass and probably another around 2 solar masses -- where the hyper limit starts growing more slowly with increased mass than it did at lower masses. Below 1 solar mass the formula is approximately (accurate +/- 5%): Hyper limit in LM = =13.7831325301 * Solar Masses + 7.3368674699 Between 1 and 2 solar masses the formula is approximately (accurate +/- 5%): Hyper limit in LM =8.6785714286 * Solar Masses + 12.6210714286 But I don't have enough data points to even approximately plot it past 2 solar masses; all I can say is the 2nd formula gives a hyper limit for class B that's 13% too large, and for class O 320% too large. (And that's assuming the smallest listd of those class stars; class B listings varied from B9 at 2.91 solar masses up to B0 at 17.8; I don't know for sure which RFC intended the chart to represent but can't imagine all of them have the same hyper limit) So there's just not enough information to even roughly guesstimate what the hyper limit of a giant black hole would be -- I can only note that the rate of increase drops off dramatically as the mass goes up, so it probably isn't insanely large. Using the clearly faulty 2nd formula (and diving the answer by 4.2 to bring it back into alignment with O class data that gives an upper bound for a million solar mass object's hyper limit at 3.9 lightyears. But that's almost assuredly several orders of magnitude too large. Still, on the scale of the vastness of space, that's pretty small. [1] From here: https://sites.uni.edu/morgans/astro/cou ... asses.html |
| Top | |
| Re: Hyper limits | |
|---|---|
|
|
|
|
munroburton
Posts: 2379
|
Thanks. That's the same chart I found and I couldn't get a straight line to fit both sets of data neatly. Mind-boggling, even if it's .04 LY. That is around 15 light-days from a black hole whose event horizon is about 2 light minutes wide. And the M87 black hole's event horizon is 2112 light minutes wide. About 1.5 light-days. |
| Top | |
| Re: Hyper limits | |
|---|---|
|
|
|
|
Joat42
Posts: 2166
|
I thought that the hyper limit was a function of a stars main sequence stellar class.
From a quick peek at a main sequence diagram, the hyper limit seem to correlate to the formula: (16 - AbsoluteMagnitude) x 2 You could probably tweak the constants a bit to get a better fit. When you look at stellar classes outside the main sequence the above doesn't fit at all. --- Jack of all trades and destructive tinkerer. Anyone who have simple solutions for complex problems is a fool. |
| Top | |
| Re: Hyper limits | |
|---|---|
|
|
|
|
munroburton
Posts: 2379
|
Absolute magnitude is a scale of brightness(at 10 parsecs distant, IIRC). It may be indirectly related to mass, but it's not a measure of mass. I've been looking around a bit and I think stellar science simply wasn't that precise in the 1990s, when RFC created the Honorverse. He possibly used the Hertzsprung-Russell diagram in some way, explaining the lack of a single straight line. If the hyper limit is based on gravitional force exerted by mass, then this should apply:  The other possible factor is the distance of the hyper limit from its generating stellar mass. Hyper limits don't have any mass, but perhaps dividing by distance squared applies somehow(eliminate mass2 from Newton's gravitional law so it doesn't throw a divide by zero error). |
| Top | |
| Re: Hyper limits | |
|---|---|
|
|
|
|
Jonathan_S
Posts: 9156
|
I think they're supposed to be non-linear to mass - otherwise how could a gas giant like Uriel have a 5 LM hyper limit; "half as deep as an M9’s". An M9 is about 0.075 solar mass. Jupiter is about 0.001 solar mass. I know HotQ says Uriel is larger than Jupiter, but I have a hard time believing that it is 37 times larger. I'm wondering if the relationship might be logarithmic, or track with the cube-root of the object's mass. I'll have to play around some more and see if I can get better fits. |
| Top | |
| Re: Hyper limits | |
|---|---|
|
|
|
|
Jonathan_S
Posts: 9156
|
No, those don't quite work
For logarithmic there's a sharp flattening of the curve from M9 through M0. Though after that point M0 - O does seem close to a line (a bit of an upward bend). 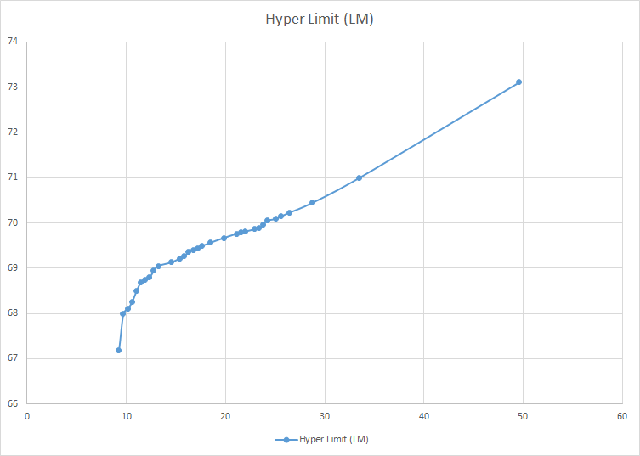 And cube root isn't right either, still some real bends. 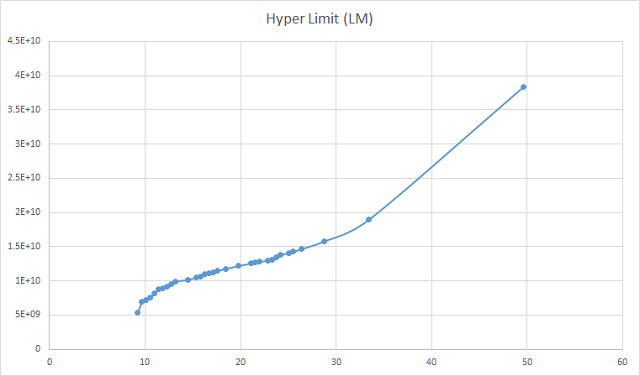 Still either of those seems a way better fits than linear |
| Top | |
| Re: Hyper limits | |
|---|---|
|
|
|
|
munroburton
Posts: 2379
|
Yeah, I agree. In UH, Jupiter's hyper limit is mentioned as 4.6 LM. Oops? |
| Top | |
| Re: Hyper limits | |
|---|---|
|
|
|
|
JohnRoth
Posts: 2438
|
Whenever something appears weird, remember that it may be there to make the story in the Honorverse work, not to make sense physically.
In this case, the story issue most likely is to keep fleets from dropping out of hyper right on a planet and demanding surrender before anyone has a chance to pick their jaw off the floor, let alone mount a defense. Assuming that's the case, the hyper limit has to be outside the habitable zone, and the habitable zone is determined by the star's size and temperature. In other words, the stellar class. Same thing applies to the giant planets: you want to keep ships leaving hyper far enough away so major installations have some time to deal with an invading fleet. |
| Top | |